Image

[Javascript] JS 中 number 的常见问题及原因

Viewed: loading...

19 minutes to read

最近看到几篇关于讲解 JS 中 number 的深度好文，文中解析了 js number 的一些常见问题，正好之前自己对这块的内容掌握不深，所以今天就刚好扩展整理一下 JS 中 number 相关的内容，跟大家分享下

诡异的 JS

首先先来看几个 JS 中不太符合常理的诡异现象

// 不同类型的 整数 小数 判等相同
console.log(42 === 42.0) // true

// Demo 1 - 乘法异常
console.log(18.9 * 100) // 1889.9999999999998
console.log(64.68 * 100) // 6468.000000000001

// Demo 2
// 典中典
console.log(0.1 + 0.2 === 0.3) // false
console.log(0.1 === 0.1) // true

// api toPrecision，配合典中典食用
(0.1 + 0.2).toPrecision(16) // '0.3000000000000000'
(0.1 + 0.2).toPrecision(17) // '0.30000000000000004'
(0.1).toPrecision(17) // '0.10000000000000001'

// Demo 3 - api toFixed 返回值反直觉
console.log(1.005.toFixed(2)) // 返回的是 1.00 而不是 1.01

// Demo 4 - 无限循环
let num = 2 ** 53
while(true) {
    if (++num % 13 === 0) {
        return num
    }
}

// Demo 5 - 数值转换
JSON.parse('{"a":180143985094813214124}') // 值少了 {a: 180143985094813220000}

// Demo 6 - 位运算异常
const a = 2 ** 31
// 1.值相等，但判等失败
console.log((a|0) === a) // false
// 2.位运算后符号异常
console.log((2 ** 31 - 1) << 1) // -2
console.log((2 ** 32 - 1) >> 1) // -1

原因所在

如果上面的现象你能够完全以自己的方式理解，那么证明你对 JS 中的 number 特性已经十分了解，就不需要看后面的内容了

如果仍有疑问，可以继续往后看具体的原因

Number 定义

JS 中只有一种数值类型： number，包括“整数”和带小数的十进制数 ——《你不知道的 JS》（中卷）

在 JS 中没有真正意义上的整数，仅拥有一个 number 类型，不像 C 拥有 int、float、double 这几种类型，这在一定程度上降低了 JS 语言的上手成本，但是也带来了一些理解上的误差

JS number 中的整数就是没有小数的十进制数，所以第一个例子也就说得通了

// 整数小数判等相同
console.log(42 === 42.0) // true

Number 实现

在 IEEE 754 中定义了 64 位双精度浮点数的标准，也就是 C 语言中的 double 类型，JS 是按照此规准来实现的 number

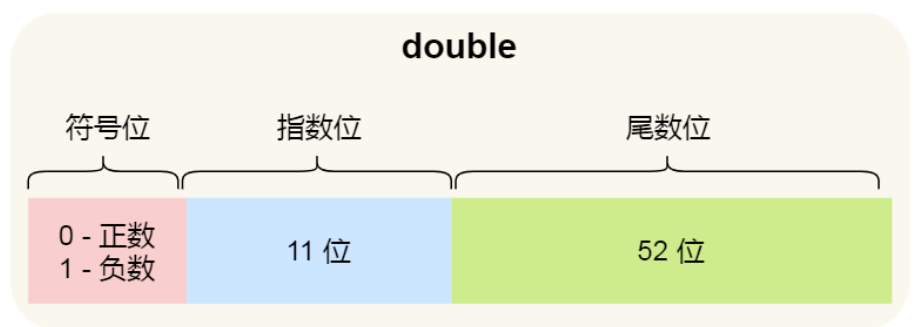
这里的具体转换过程我们后面详细演示，这里先铺垫介绍下 64 位表示法的设计方案，它由符号位，指数位和尾数位组成（这里也看出了前人对如何使用最小的空间表示最多的数字范围的权衡思考，如果让大家来设计，不知道有没有更好的思想呢）：

picture 2

Number 运算

在前面的介绍中我们不难发现，JS 作为一门高级脚本语言，对于 number 类型的设计是比较宽松的，使用一个类型就支持了所有的数值，但是与之而来的代价就是较大的字节空间占用和较长运算时间

接下来我们详细看看，JS（或者大多数编程语言）对于 number 数值的运算转换流程，相信分析过后，对于前面列举的很多诡异现象都能够有更好的理解

运算流程主要有以下几步：

1. 十进制转二进制

这里以十进制为例，把带小数的十进制数 106.6953125 转换成二进制，来看看详细的流程

106 / 2 = 53  ...... 0
53  / 2 = 26  ...... 1
26  / 2 = 13  ...... 0
13  / 2 = 6   ...... 1
6   / 2 = 3   ...... 0
3   / 2 = 1   ...... 1
1   / 2 = 0   ...... 1
结果为得到的余数按照从后往前排列   1101010
0.6953125 x 2 = 1.390625  ...... 1
0.390625  x 2 = 0.78125   ...... 0
0.78125   x 2 = 1.5625    ...... 1
0.5625    x 2 = 1.125     ...... 1
0.125     x 2 = 0.25      ...... 0
0.25      x 2 = 0.5       ...... 0
0.5       x 2 = 1         ...... 1
结果为得到的整数位按照从前往后排列   1011001

这里转换后获得的二进制是：1101010.1011001

2. 二进制转科学计数法

1101010.1011001 转为 1.1010101011001 * 2^6，这里进行转换的目的也是为了使用尽可能少的数字来表示对应的 number 值

这里举得带小数的例子尾数比较长，可能看不出来压缩位数的效果。假设需要转换的是 1000000 这个二进制值，那么科学计数法就变成了 1 * 2^6，只需要 1 和 6（二进制 110），我们就能知道原数为 10000 了

那么根据前文的定义，我们可以知道，这里的指数值为 6

3. 转换成 JS 支持的存储格式【重点】

根据前文对于双精度类型格式的介绍，我们在这个例子上对其展开说明下其定义的内容：

picture 3

综上，可以归纳为这样的数学转换表达式【数学之美了】

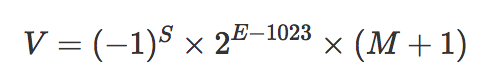
picture 4

根据上面的规则，我们分析 1.1010101011001 * 2^6 可以得出

最终转换结果如图

picture 5

4. 进行运算

我们上面举的例子，大家可以发现，最后的尾数位是没有无限循环的，这就证明了这个数据能够比较好的被二进制表达，没有误差，所以误差问题没有暴露出来

这里我们就以前文中的几个 demo 为例，看看运算过程

demo 1
// 乘法异常
console.log(18.9 * 100) // 1889.9999999999998
console.log(64.68 * 100) // 6468.000000000001

我们仔细看看这个例子不难发现，都是乘以 100，结果一个比应有结果小，一个比应有结果大，我们来看看原因是啥

首先 18.9 这个十进制数，我们按照前文的方法来计算一遍，结果如下

picture 6

不难发现，尾数部分是无限循环的，舍弃后面的数字必然导致转换后的值比现在小，再通过乘法放大，结果也就说的通了

那 64.68 经过计算后为啥还大了呢，这里看看二进制的转换结果

picture 7

发现依然有数据丢失，但是根据 JS 引擎定义的规则，最后丢失的值会进行 0 舍 1 入

64.68 转为二进制后是 1000000.10101110000101000111101011100001010001111011，但实际上 64.68 尾数部分的二进制真实的是 10101110000101000111 (无限循环)，受存储空间限制，存储策略使最后四位从原本的 1010 变为 1011，所以存储在 JavaScript 中的数比数学意义上的 64.68 会大

所以由于精度问题，结果可能会比预期中的大或者小，都是合理的

demo 2
// 典中典
console.log(0.1 + 0.2 === 0.3) // false
console.log(0.1 === 0.1) // true

这个问题实在太经典了，我们来看看

由于 0.1、0.2、0.3 都无法准确地用二进制表示，所以都存在一定的误差：

通过计算之后，我们页可以发现结果确实并不相同，所以两者不相等是合理的

但是，真的就是这么简单吗？

我们来看看精度相关的这个例子，不知道大家有没有发现端倪

toPrecision 以指定的精度返回该数值对象的字符串表示，从左至右第一个不为0的数开始数起

// api toPrecision，配合典中典食用
(0.1 + 0.2).toPrecision(16) // '0.3000000000000000'
(0.1 + 0.2).toPrecision(17) // '0.30000000000000004'
(0.1).toPrecision(17) // '0.10000000000000001'

这里我们发现

在十进制下，0.1 + 0.2 的第 17 位精度值结尾有 4，0.1 的结尾也有 1，那么既然 0.1+0.2 !== 0.3，那么为什么 0.1 === 0.1 呢？

这里就要分析下，双精度浮点数是按照什么规则来截断的了

The 53-bit significand precision gives from 15 to 17 significant decimal digits precision (2−53 ≈ 1.11 × 10−16). If a decimal string with at most 15 significant digits is converted to IEEE 754 double-precision representation, and then converted back to a decimal string with the same number of digits, the final result should match the original string. If an IEEE 754 double-precision number is converted to a decimal string with at least 17 significant digits, and then converted back to double-precision representation, the final result must match the original number.[1]

维基百科中这段话解释了规则，简单来说，就是如果当 17 位有效数字的十进制数字字符串转回双精度浮点数时，和之前的相同，那么取最短的十进制数即可

这里 0.1 和 0.10000000000000001 转成双精度浮点数的存储是一样的，所以取 0.1 即可

但是 0.1 + 0.2 不满足，所以不等于 0.3

demo 3

toFixed 使用定点表示法来格式化一个数值

// api toFixed 返回值反直觉
console.log(1.005.toFixed(2)) // 返回的是 1.00 而不是 1.01

按照常理来说，应该是四舍五入，获取 1.01 的结果才对，这里为什么是 1.00 呢，我们还是得看下二进制表示结果

picture 8

转换为十进制之后的结果是 1.00499999999999989341858963598，当这个时候我们再次调用 toFixed(2)，小数点后第二位为零，第三位为 4，所以被舍弃掉了，这也是一个由精度影响的结果

扩展知识

怎么解决上面发现的误差问题

核心思想主要是 对有效数字进行控制 或者 将数字转换成字符串进行运算

JS 安全的 number 的数值范围

这里的安全，指的是双精度数和十进制数能够一一对应。超过这个范围，会有两个或更多整数的双精度表示是相同的；反过来说，超过这个范围，有的整数是无法精确表示的，只能 round 到与它相近的浮点数（说到底就是科学计数法）表示，这种情况下叫做不安全整数

在 JS 中，官方给出的安全值范围如下：

那么实际范围就是 [2 ** 53 - 1, -1 * (2 ** 53 - 1)]

那么为啥是 53 呢，因为二进制表示中，有效数字最长为53个二进制位（ 52 位尾数 + 有效数字第一位的 1[被舍弃的 1] ）

举个例子：

但是对于 2^53^ + 1 的存法就出现了问题：符号位：0，指数：53，尾数：1.00000…000（一共52个0），这个值的结果和 2^53^ 一样

所以这也说明了为什么安全范围不包括边界，同时也解释了为什么 demo 4 会无限循环了

// Demo 4 - 无限循环
let num = 2 ** 53
while(true) {
    if (++num % 13 === 0) {
        return num
    }
}

demo5 中的 180143985094813214124 => 180143985094813220000 也是因为数据超出安全范围，导致双精度结果和其他数字重叠，导致结果异常

原数二进制表示

picture 9

转换后的异常数的二进制表示

picture 10

一模一样，神仙都分不出来

大数危机

从前面的讲解中，我们不难发现，如果二进制的结果一样，那么根本无法用十进制的数完全无法与二进制一对一的表示

我们在实际可支持的数字表示范围中，安全的仅仅占很小一部分，所以称为大数危机

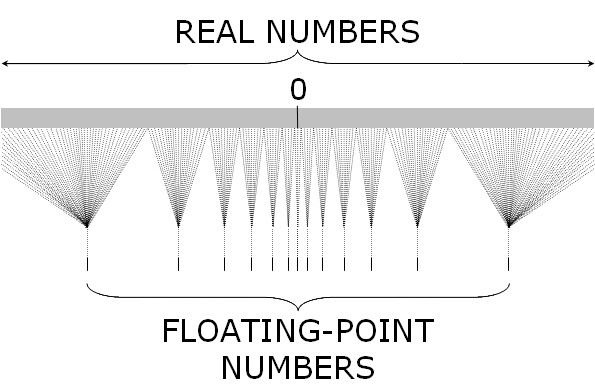
picture 11

上图中的双精度范围为（-2^1024^ ~ 2^1024^）[下方的 Floating-Point Numbers]

我们使用的 (-2^53^ ~ 2^53^）只占真实 number 中的很小一部分

位运算

In Java, the bitwise operators work with integers. JavaScript doesn’t have integers. It only has double precision floating-point numbers. So, the bitwise operators convert their number operands into integers, do their business, and then convert them back. In most languages, these operators are very close to the hardware and very fast. In JavaScript, they are very far from the hardware and very slow. JavaScript is rarely used for doing bit manipulation. — Douglas Crockford in “JavaScript: The Good Parts”, Appendix B, Bitwise Operators (emphasis added)

从上面的引用中也能发现，JS 中的位运算其实是做了一层包装的：并不是简单的位运算，而是做了一层转换在其中

除此之外还有一些补充的位运算规则：

1. 值相等但判等失败
const a = 2 ** 31
console.log((a|0) === a) // false

这里看上去一个正整数，进行按位或，理论上没啥问题对吧，但是按位或的结果却并不是原始值

(2 ** 31) | 0 // -2147483648
Number(2 ** 31).toString(2) | 0 // 0

这里的原因主要是位运算仅支持 32 位导致的

原来的 2 ** 31 的二进制表示如下 10000000000000000000000000000000，进行按位或时，1 当成了符号位，自然结果会是 0 或者 负的 2^31^

2.位运算后正数变负数
console.log((2 ** 31 - 1) << 1) // -2

这里的原因依然是仅支持 32 位运算导致的，二进制原数为 01111111111111111111111111111111，左移一位后，变成了 11111111111111111111111111111110，导致变成了 -2

console.log((2 ** 32 - 1) >> 1) // -1

同理，原数为 1111111111111111111111111111111(31位，开头的 0 省略了)，右移后变成 11111111111111111111111111111111(32位，开头补充了个 1)，导致结果变成 -1

ES6 语法中的 BigInt

在新的 ES6 语法中，JS 新增了 BigInt 类型的变量来支持安全范围外的数字

可以用在一个整数字面量后面加 n 的方式定义一个 BigInt ，如：10n，或者调用函数BigInt()

const theBiggestInt = 9007199254740991n;

const alsoHuge = BigInt(9007199254740991);
// ↪ 9007199254740991n

const hugeString = BigInt("9007199254740991");
// ↪ 9007199254740991n

const hugeHex = BigInt("0x1fffffffffffff");
// ↪ 9007199254740991n

const hugeBin = BigInt("0b11111111111111111111111111111111111111111111111111111");
// ↪ 9007199254740991n

个人理解是官方将上述的第三方库以 polyfill 的方式注入到了 BigInt 中，进行了整合而提供的，本质上应该没有区别

结语

这篇文章参考了很大多大佬的回答和文章，综合了目前可能会遇到的 number 相关的问题和原理，希望能够帮助大家理解和掌握这块的内容

感慨一下，计算机的世界真的是充满数学之美

参考文档

Comments

There are comments.

📰 邮箱订阅 📰
不错过每篇更新~
如有发现问题，请点击这里勘误🐶